Introduction à la statistique descriptive
La statistique a pour objet de recueillir des observations portant sur des sujets présentant une certaine propriété et de traduire ces observations par des nombres qui permettent d’avoir des renseignements sur cette propriété.
Le but de la statistique descriptive est de structurer et de représenter l’information contenue dans les données, de décrire de façon synthétique et parlante des données observées pour mieux les analyser.
Avant de les représenter, il est important de bien comprendre la nature des données.
Commençons donc par un peu de cours pour reprendre ces notions.
Premiers exercices reprenant les définitions fondamentales de statistique descriptive
Exercice 1
Une enquête sur la pratique des jeux vidéo chez les jeunes de 12 à 16 ans a été menée en notant le genre (fille ou garçon), l’âge exact, ainsi que la dépense mensuelle consacrée aux jeux vidéo. Parmi les conclusions du sondage, on note les informations suivantes :
- 62% des jeunes déclarent posséder (ou avoir accès chez eux à) un ordinateur,
- 480 jeunes déclarent posséder une console, 525 déclarent ne pas en posséder,
- 37% affirment jouer souvent (à des jeux vidéo), 12% rarement, 46% de temps en temps et 5% jamais.
Êtes-vous d’accord avec les affirmations suivantes ? Justifiez chacune de vos réponses.
- Dans cette situation statistique, l’individu est un jeu vidéo. Réponse
- Dans cette situation statistique, l’individu est un jeune qui joue à un jeu vidéo. Réponse
- Dans cette situation statistique, l’individu est un jeune de 12 à 16 ans. Réponse
- Dans cette situation statistique, la population visée est celle des jeunes ayant une console pour jouer. Réponse
- On a choisi de ne prendre qu’un échantillon pour laisser les jeunes jouer. Réponse
- Tous les jeunes de Montpellier ont été interrogés. Réponse
- L’échantillon est de taille 1005. Réponse
Exercice 2
La Société Nationale des Bois (SNB), dont l’activité est l’aménagement de la forêt, la production forestière, la transformation de la ressource forestière et le négoce de bois, cherche à mieux connaître les besoins de ses clients.
Elle interroge par conséquent l’ensemble de ses clients et relève les informations ci-après :
- la domiciliation du client par continent : "Afrique", "Asie/Océanie", "Amériques", "Europe",
- le montant total des commandes à la SNB sur l’année 2020 exprimé en euros,
- le volume total des achats sur l’année 2020 exprimé en m3 de bois,
- l’utilisation principale du bois : "mobilier", "construction/charpente", "menuiserie intérieure/ parquet", "œuvres d’art/ instruments de musique", "autre",
- le nombre de commandes dans l’année 2020,
- l’essence de bois commandée principalement : "okoume", "ozigo", "bois divers",
- le niveau de satisfaction à l’égard des services de la SNB : "très satisfait" (1), "assez satisfait" (2), "moyennement satisfait" (3), "peu satisfait" (4), "mécontent" (5)
- souhaitez-vous une plus grande diversification des essences proposées : oui/non ?
- quelle est votre prévision d’achat pour l’année 2021 en euros ?
Êtes-vous d’accord avec les affirmations suivantes ? Justifiez chacune de vos réponses.
- On a observé 12 variables. Réponse
- Il y a exactement 2 variables qualitatives nominales. Réponse
- Il y a exactement 3 variables quantitatives continues. Réponse
- Il n’y a pas de variable quantitative discrète dans cette enquête. Réponse
- Il n’y a pas de variable qualitative ordinale dans cette enquête. Réponse
- Il y a une variable dichotomique. Réponse
- L’ensemble de toutes les variables qualitatives nominales engendre au total 14 modalités. Réponse
Exercice 3
À partir d'un questionnaire, il a pu être mesuré le degré́ de satisfaction d’un échantillon de clients d'un site de e-commerce. Les résultats suivants ont été́ obtenus :
0121330212
3332102011
3232212203
1312033121
2021232123
0231210203
- Décrire la situation statistique. Réponse
- Réordonner la liste des réponses. Réponse
- Construire le tableau de la distribution en effectifs et en fréquences. Réponse
- Donner les valeurs de x5, x27, x(5) et x(27). Réponse
Exercice 4
4 candidats se présentent à une élection locale. Les résultats sont donnés dans le tableau suivant :
| Candidats | A | B | C | D |
| % de voies obtenues | 26,56 | 34,65 | 20,43 | 18,36 |
Introduction au graphes de distribution et distribution cumulée
Nous nous demandons dans cette section comment visualiser graphiquement la répartition des individus sur les modalités d’une variable.
Les chiffres et statistiques sont parfois utilisés à mauvais escient dans la presse, la publicité ou le monde politique, par erreur ou par manipulation délibérée. De son côté, le public peine parfois à appréhender ces données. Les experts parlent même d’innumérisme, l’équivalent mathématique de l’illettrisme.
Commençons par une liste de cas problématiques issus des sites et lemonde et letemps.ch présentés ici. Il est important que vous soyez critiques quand vous rencontrez de telles visualisations !
À chaque type de variables correspond un graphe particulier que nous allons décrire dans ce cours.
Dans cet exercice, vous utilisez le classeur comptoir.xls. Il est constitué de 8 feuilles :
- Produits décrit les produits vendus ainsi que leur disponibilité en stock,
- Clients contient les coordonnées des clients de d’entreprise,
- Commandes contient l’ensemble des informations sur les commandes (date de livraison, adresse de livraison, ...),
- Détails_commandes contient des détails sur les contenus des différentes commandes,
- Catégories liste les catégories des différents produits vendus,
- Employés contient toutes les informations utiles sur les employés de l’entreprise,
- Fournisseurs contient toutes les informations utiles sur les différents fournisseurs,
- Messagers contient les coordonnées des transporteurs.
Partie 1 : Premiers calculs
- Dans la feuille Détails_commandes, après avoir fixé les volets pour visualiser le haut et le bas de la feuille simultanément, calculer à l’aide de la fonction SOMMEPROD le montant total en euros de toutes les commandes avant les remises éventuelles, le montant total en euros de toutes les remises accordées et, pour finir, le chiffre d’affaire réalisé.
- Dans la feuille commandes, calculer le délai moyen entre la date d’envoi et la date d’émission d’une commande. Calculer la proportion de commandes pour laquelle ce délai dépasse 20 jours.
Partie 2 : des tris
- Trier la feuille employé pour connaître le plus ancien et le plus récent par ordre croissant de date d’embauche.
- Trier par ordre alphabétique de pays, de ville puis de nom la feuille Clients.
Partie 3 : Sous totaux
- Dans la feuille Détails_commandes (que vous aurez pris soin de dupliquer), calculer à l’aide de la fonction sous-totaux du menu données, le montant total de chaque commande après remise.
- Vérifier que le chiffre d’affaire trouvé correspond bien à celui que vous aviez calculé lors de l’exercice 1.
Partie 4 : Premiers graphiques
- Ajouter une feuille frais de port par pays et remplissez la avec la liste ci-dessous.
Argentine
Autriche
Belgique
Brésil
Canada
Danemark
Espagne
Etats-Unis
Finlande
France
Irlande
Italie
Mexique
Norvège
Pologne
Portugal
Royaume-Uni
Suède
Suisse
Venezuela
- Calculer à l'aide de la fonction SOMME.SI le total des frais de port par pays puis représenter cette information sous la forme d'un diagramme secteur.
- Dans la feuille produit, calculer la différence de prix entre l'année 2021 et 2020. Pour la catégorie 1 de produit (réaliser un tri), afficher le diagramme en barre d'évolution du prix.
- Dans la feuille employés, à partir des notes d'évaluation d'aptitudes, réaliser un diagramme radar pour comparer les employés.
Partie 5 : Les tableaux croisés dynamiques (TCD)
Avec les tableaux croisés dynamiques, on relie des données entre elles afin d’en dégager des informations synthétiques.
Dans notre cas pratique, on peut ainsi répondre à une question du type : dans quels pays, chacun des employés arrive à vendre le plus ?
Les données source d'un TCD doivent obligatoirement être ordonnées de la façon suivante :
- la première ligne doit contenir une étiquette par colonne
- chaque colonne ne doit contenir qu'un seul type de données.
Parcourir les menus pour trouver la fonction Tableaux Croisés Dynamiques.
- À partir de la feuille Détails_commandes, calculer à l’aide d’un TCD le nombre total de chaque produit commandé. Calculer les rangs des produits dans l’ordre décroissant des quantités vendues (à l’aide de la fonction prédéfinie RANG).
- À partir de la feuille Détails_commandes, établir le tableau croisé dynamique qui donne pour chaque fournisseur, la somme des quantités en stocks de chaque catégorie de produits.
- À partir de la feuille Produit, créer un TCD qui calcule pour chaque employé le nombre de commandes passées dans les différents pays. Identifier le meilleur vendeur ainsi que le pays avec lequel le plus de commandes a été passé. Constituer un graphique de ces données synthétiques.
La correction de cet exercice est disponible ici.
Introduction aux indices simples et quantiles
La construction d’indices statistiques vise à résumer la distribution de la variable, i.e. la répartition des valeurs observées.
Les valeurs étant numériques, on peut alors s’intéresser à résumer la distribution de 2 façons :
- la localisation : reflète un endroit de l’échelle autour duquel se situent les valeurs observées → une « position » sur l’échelle
- la dispersion : renseigne sur l’éloignement des valeurs observées les unes par rapport aux autres. → un « écartement » sur l’échelle
Ces 2 types d’indices renseignent sur des notions très différentes.
Commençons par un peu de cours.
Exercices
Télécharger le jeu de données ici.
Il est essentiel de bien comprendre chaque variable avant tout traitement des données.
- "acc" pour le nombre d'accidents observés dans le mois
- "tmax" pour la moyenne des températures maximales journalières observées dans le mois
- "tmin" pour la moyenne des températures minimales journalières observées dans le mois
- "tmoy" pour la moyenne des températures moyennes journalières observées dans le mois
- "tcon" pour la moyenne des températures de condensation journalières observées dans le mois
- "sol" pour la moyenne des quantités de soleil journalières observées dans le mois
- "plui" pour la moyenne des quantités de pluie journalières observées dans le mois
- "neig" pour la moyenne des quantités de neige journalières observées dans le mois
- "jour" pour le nombre de jours du mois
Pour chaque variable vous allez calculer :
- la taille de l'échantillon
- le max,
- le min,
- l'étendue,
- la moyenne,
- la variance,
- l'écart-type,
- la médiane,
- les 2 quartiles,
- les 2 déciles D3 et D6,
- les 2 centiles C1 et C69
Pour la variable tmax, tracer le diagramme « Boites à moustaches ».
La correction de cet exercice est disponible ici.
Introduction au test de Khi 2
Un test du khi2 est un test d'hypothèse qui compare la loi de distribution observée de vos données à une loi attendue.
Il existe plusieurs types de tests du khi2. Dans cette rapide introduction, nous allons nous intéresser aux Tests d'indépendance qui permettent de déterminer si la valeur observée d'une variable dépend de la valeur observée d'une autre variable. Par exemple, vous pouvez vérifier si le vote d'une personne pour un candidat est indépendant du sexe de l'électeur.
Commençons par un peu de cours.
Test du khi2 (ou khi carré)
Dans cet exercice, nous travaillons sur des données issues d’une enquête menée par une DRH qui s’interroge sur le lien entre le sexe des employés et le stress ressenti au travail. Les données de cet exercice sont disponibles ici. Dans le tableau de données, dans la colonne sexe, un 1 signifie homme et un 0 signifie femme. Dans la colonne stress, un 1 signifie que l’individus s’est déclaré stressé et un 0 non.
Nous allons voir comment réaliser un test du khi2. Il s’agit d’un test d’indépendance entre deux variables. Pour réaliser le test du khi2 (ou khi carré) nous allons effectuer 5 étapes :
- Réaliser un tableau croisé dynamique
- Calculer les fréquences théoriques
- Calculer le khi2
- Rechercher le khi2 (ou khi carré) critique
1 – Réaliser un tableau croisé dynamique
Nous allons construire un tableau croisé dynamique pour connaitre la répartition des deux variables (les deux réponses de formulaires). Ainsi, nous serons, combien de femmes ont répondu oui ou non et combien d’hommes ont répondu oui ou non. Le tableau à obtenir doit ressembler au tableau ci-dessous.
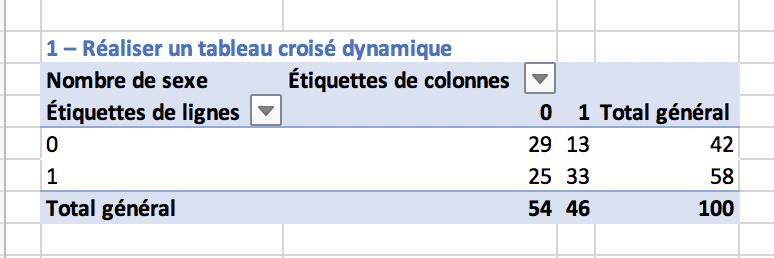
2 – Calcul des fréquences théoriques
Les fréquences théoriques correspondent aux fréquences que l’on obtiendrait si nos deux variables étaient indépendantes. Autrement dit, sans lien entre nos variables sexe et stress, nous devrions logiquement obtenir le même pourcentage de réponses positives et négatives chez les hommes et chez les femmes.
- Copiez/collez le tableau croisé dynamique que nous avons créé précédemment, et remplacer dans les entêtes des lignes et des colonnes les 0 et 1 par les véritables noms des variables correspondantes.
- Calculer le pourcentage des personnes ayant répondu oui ou non à la question sur le stress. Nous obtenons le résultat ci-dessous.

- Calculer les fréquences théoriques dont nous aurons besoins pour le calcul du khi2. Pour cela, recopier le tableau ci-dessus sans les pourcentages que nous venons de calculer. La capture ci-dessous montre comment obtenir les fréquences théoriques, pour la réponse oui des femmes.
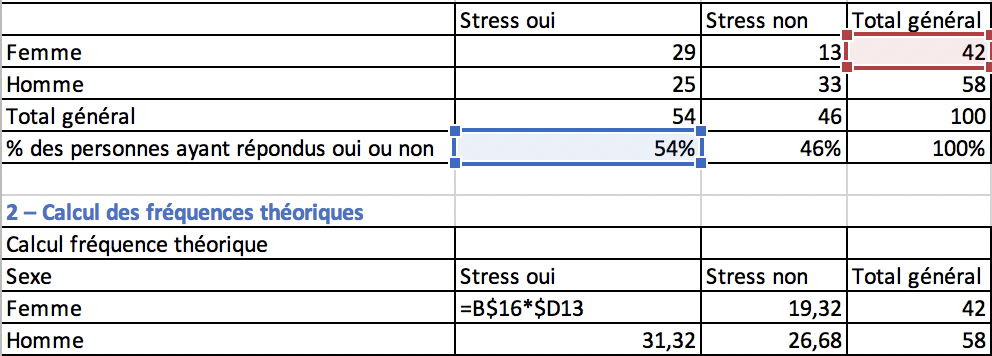
Le résultat est le suivant :

3 – Calcul du khi2
Nous allons passer au calcul du khi2. Il faut une nouvelle fois recopier le tableau.
- Pour effectuer le calcul du khi2, sélectionner la case du oui au stress pour les femmes, et y insérer la formule qui va calculer la portion du khi2 pour les femmes ayant affirmé être stressées sur leur lieu de travail selon la formule
(femmes_stressées – freq_theorique_femmes_stressées)² / freq_theorique_femmes_stressées
En Excel, le chapeau suivi du deux permet de calculer le carré.
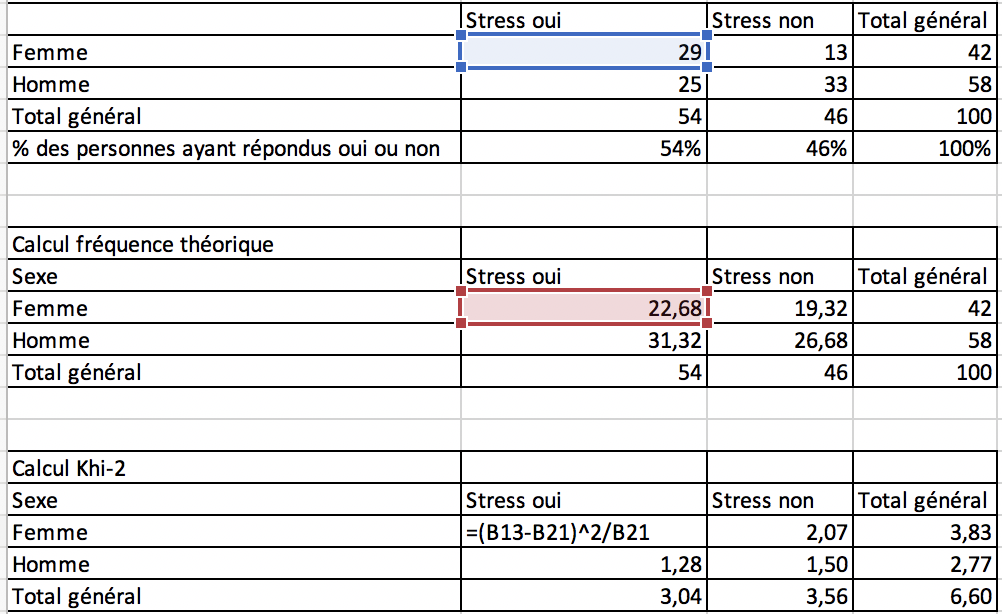
Pour calculer les colonnes total, il suffit de faire pour chaque colonne du tableau la somme et de même pour chaque ligne. Le khi2 apparaît dans la somme des colonnes et lignes « total » : 6,60.

4 – Recherche du khi2 critique
Nous allons maintenant pouvoir tester l’indépendance de nos variables. Pour cela, nous allons rechercher la valeur critique du khi2. Nous formulons deux hypothèses :
- L’hypothèse H0 indique qu’il n’y a PAS DE LIEN entre les variables sexe et stress sur le lieu de travail.
- L’hypothèse H1 indique qu’il n’y a UN LIEN entre les variables sexe et stress sur le lieu de travail.
Nous allons calculer deux valeurs du khi2 critique avec la fonction KHIDEUX.INVERSE. Cette fonction prend deux paramètres :
- La probabilité représente le seuil de signification, généralement on utilise 5%, soit 0,05. Il s’agit du risque d’erreur que l’on est prêt à accepter.
- Pour le degré de liberté, il faut utiliser la formule : dl = (nombre de catégories de la 1 variable – 1) * (nombre de catégories de la 2ème variable – 1).
Dans notre cas, chaque variable compte deux catégories (hommes / femmes et la réponse oui / non) donc cela donne dl = (2-1) * (2-1) = 1 * 1 = 1. Notre degrés_liberté est donc 1.
Le résultat avec le paramètre probabilité à 5% (donc 0,05) est 3,841458821.
Les conclusions que l’on peut en tirer sont les suivantes :
- Avec un risque d’erreur de 5%, comme notre khi2 6,60 est supérieur à 3,84 alors on rejette H0, c’est-à-dire on rejette le fait qu’il n’y est pas de lien entre les variables. On peut ainsi conclure qu’il existe un lien entre le sexe des répondants et la réponse à notre question sur le stress sur le lieu de travail.
- Et finalement ? Existe-t-il un lien entre les deux variables ? On peut répondre oui à un seuil de signification de 5%.
Une correction de cet exercice est disponible ici.