Autour de données aléatoires
Dans cette page, nous vous proposons un exercice de synthèse. Nous allons voir comment utiliser de manière basique l'outil « tableau croisé dynamique ». Nous allons aussi voir comment créer des séries et comment des données aléatoires peuvent être générées (cela peut être utile pour réaliser des ensembles de test).
Créer une série
Dans ce préambule, nous voulons pouvoir générer dans la première colonne d'un nouveau classeur, les entiers à partir de 0, multiples de 3, inférieurs à 7000. Plusieurs méthodes sont possibles.
- Première méthode : utilisation du mécanisme de copie incrémentale (si vous avez besoin de révision, vous pouvez consultez la partie
Poignée de recopie
du TD B2 de niveau Standard. - Deuxième méthode : formule, puis copier-coller ou recopier vers le bas.
- Troisième méthode : utiliser l'outil de création de séries (avec Microsoft Excel, il faut saisir la première valeur avant de lancer le remplissage via le menu Édition > Remplissage > Série… ou dans l'onglet d'accueil du ruban ; avec OpenOffice et Libre Office, il faut pré-sélectionner la zone à remplir avant de lancer le remplissage via Édition > Remplir > Série… pour OpenOffice et via Feuille > Remplir les Cellules>Remplir la série pour LibreOffice.
Les deux premières méthodes nécessitent de connaître la valeur du dernier multiple de 3 inférieur à 7000 et d'être capable de trouver le numéro de la ligne correspondante. En pratique, la troisième méthode est sans doute à privilégier.
- Ouvrez un nouveau classeur.
- Dans la première feuille, placez dans une les entiers à partir de 0, multiples de 3, inférieurs à 7000.
- Testez les 3 méthodes précédentes.
- Conservez une seule colonne (la première) avec les entiers à partir de 0, multiples de 3, inférieurs à 7000.
- Une fois ceci réalisé, insérez dans la première cellule de cette colonne (sans supprimer de valeur) l'intitulé « Identifiant » et pensez, pour la suite, à utiliser les volets.
Générer des données aléatoires
- Dans la deuxième colonne, utilisez la fonction ALEA.ENTRE.BORNES pour définir un contenu aléatoire entier compris entre 1 et 10 pour toutes les lignes. Vous intitulerez cette colonne « Aléa ».
- Utilisez un collage spécial pour ne coller que les valeurs de cette deuxième colonne dans la troisième colonne que vous intitulerez « Valeurs ».
- Fermez le fichier, puis rouvrez-le et comparez les colonnes B et C. Dans la suite, on ne travaillera pas sur la colonne B.
Remarque : si vous travaillez avec Libre Office, il existe une fonctionnalité pré-définie pour remplir des cellules avec des nombres aléatoires. Choisissez le menu Feuille > Remplir les cellules > Remplir de nombres aléatoires…, puis précisez la plage de cellules concernée et les caractéristiques des nombres aléatoires attendus (cela ne semble pas exister avec Microsoft Excel ni dans Open Office).
Calcul des fréquences
Calcul 1
Dans la feuille 2 de votre classeur, créez un « tableau croisé dynamique » calculant, pour chaque valeur de 1 à 10, son nombre d'occurrences dans la colonne C de la première feuille, puis un second « tableau croisé dynamique » indiquant le pourcentage d'apparition de chacune de ces valeurs. Vous obtiendrez des tableaux ressemblant à
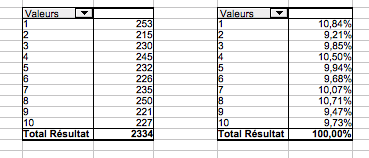
Calcul 2
En utilisant la fonction NB.SI
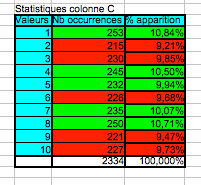
Refaites le même travail que précédemment, mais sans utiliser l'outil « tableau croisé dynamique » et en regroupant les deux calculs dans un seul tableau.
De plus, le fond de couleur des cellules sera vert si le nombre d'occurrences est strictement supérieur à 230 et rouge sinon (utilisez le formatage conditionnel de cellules).
Votre tableau aura la présentation suivante :
Aléatoire ?
Est-ce que vous trouvez que les données sont suffisamment équiréparties ? (d'après la loi des grands nombres, les fréquences devraient toutes tendre vers 10% quand le nombre de valeurs tirées aléatoirement tend vers l'infini)

